Le but de ce chapitre est de savoir conjecturer un lien possible entre deux caractères .
Ce domaine est utile pour estimer une évolution future ou pour montrer que deux notions
sont peut-être corrélées.
Statistiques à deux variables
Dans toute la suite du chapitre, nous travaillerons avec les deux exemples suivants :
-
le lien entre l'année et le trafic mondial de données sur le réseau mobile en Exaoctets.
-
le lien entre la production d'électricité au Japon avec la distance entre la Lune et Uranus.
-
Le lien entre le nombre diplômé.e.s en Master de mathématiques et statistiques aux États-Unis avec le nombre de programmeurs informatiques en Californie.
Premier exemple concret
Voici le trafic mondial de données ayant transité sur le réseau mobile en Exaoctets (c'est-à-dire en
milliards de Gigaoctets) suivant les années considérées.
Ces valeurs mesurées ou estimées sont issues d'une étude de l'équipementier
Ericsson,
étude citée dans le rapport publié en juillet 2024, par la Conférence de Nations Unis pour le Commerce Et le Développement (la CNUCED),
rapport portant sur les différentes pollutions engendrées par les secteurs du numérique,
cf. page 34 de ce rapport.
| année | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 | 2028 | 2029 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Trafic | 26.53 | 39.39 | 58.21 | 83.75 | 109.73 | 136.6 | 174.48 | 218.5 | 270.5 | 328.89 | 394.09 | 466.16 |
On peut par exemple se poser les questions suivantes :
-
Est-ce qu'il semble y avoir un lien entre l'année considérée et le trafic mondial ?
-
Est-ce que l'on pourrait en déduire une estimation fiable du trafic en 2034 ?
Deuxième exemple concret
On a mesuré entre 1980 et 2021 :
-
La distance moyenne entre Uranus et la Lune (en Unité Astronomique, c'est-à-dire la distance moyenne entre la Terre et le Soleil), moyenne calculée sur la distance du premier jour de choix mois de l'année considérée.
-
La production électrique au Japon en milliards de kWh.
Le données sont fournies dans les tableaux ci-dessous et sont issues respectivement du site Astropy utilisant des programmes en Python pour calculer des données astronomiques et de l'Administration États-unienne informant sur l'énergie (EIA) :
| année | 1980 | 1981 | 1982 | 1983 | 1984 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance | 18.7389 | 18.7982 | 18.8636 | 18.9279 | 18.9951 | 19.0599 | 19.1244 | 19.1902 | 19.2579 | 19.3212 | 19.3877 |
| Production | 546.764 | 546.029 | 553.199 | 586.835 | 618.331 | 638.364 | 643.521 | 693.668 | 725.328 | 763.506 | 813.348 |
| année | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance | 19.4535 | 19.5176 | 19.5817 | 19.6425 | 19.6999 | 19.7555 | 19.8053 | 19.8512 | 19.894 | 19.9294 | 19.9645 |
| Production | 840.404 | 848.558 | 856.06 | 911.02 | 935.922 | 955.009 | 985.076 | 991.287 | 996.945 | 983.184 | 965.017 |
| année | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
|---|---|---|---|---|---|---|---|---|---|---|
| Distance | 19.9955 | 20.0212 | 20.0443 | 20.0666 | 20.0823 | 20.0961 | 20.1015 | 20.1059 | 20.1047 | 20.0959 |
| Production | 982.598 | 973.485 | 1001.92 | 1011.13 | 1028.62 | 1069.04 | 1003.21 | 974.935 | 1079.22 | 1044.07 |
| année | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
|---|---|---|---|---|---|---|---|---|---|---|
| Distance | 20.0797 | 20.0648 | 20.0405 | 20.0136 | 19.9804 | 19.9478 | 19.9116 | 19.8719 | 19.8254 | 19.7836 |
| Production | 1043.55 | 1027.43 | 1027.24 | 1003.03 | 1002.32 | 1005.87 | 1008.91 | 988.982 | 960.785 | 954.857 |
On peut par exemple se poser les questions suivantes :
-
Est-ce qu'il semble y avoir un lien entre la production électrique et la distance Lune-Uranus ?
-
Est-ce que l'on pourrait en déduire une estimation fiable de la production en 2028 ?
Troisième exemple concret
Voici entre 2012 et 2021 le nombre d'étudiant.e.s diplômé.e.s d'un Master en mathématiques et
statistiques aux États-Unis ainsi que le nombre de programmeurs informatiques en Californie.
Les premières valeurs sont issues d'une étude du
Centre National pour les Statistiques sur l'Éducation (NCES) des États-Unis.
Les secondes valeurs sont issues d'une étude du
Bureau des Statiques sur l'Emploi (BLS) des États-Unis.
| année | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
|---|---|---|---|---|---|---|---|---|---|---|
| Diplômé.e.s | 6246 | 6957 | 7273 | 7589 | 8451 | 9082 | 10443 | 11382 | 12041 | 12583 |
| Nombre de programmeurs informatiques | 41540 | 38750 | 37990 | 38650 | 37570 | 34050 | 29740 | 24400 | 21800 | 23960 |
On peut par exemple se poser la question suivante :
Est-ce qu'il semble y avoir un lien entre le nombre de Masters délivrés et le nombre de programmeurs informatiques en Californie ?
Ce sont trois exemples de séries statistiques à deux variables :
On considère deux caractéristiques $x$ et $y$ d'une même population.
On définit une série statistique à deux variables $x$ et $y$
prenant les valeurs $x_1$, ..., $x_i$, ... $x_n$ et $y_1$, ..., $y_i$, ... $y_n$ par un
tableau comme celui-ci :
| Première variable $x$ | $x_1$ | ... | $x_i$ | ... | $x_n$ |
|---|---|---|---|---|---|
| Seconde variable $y$ | $y_1$ | ... | $y_i$ | ... | $y_n$ |
Dans ce chapitre, nous chercherons à voir comment évaluer s'il existe un lien mathématique (une corrélation) entre deux telles variables.
Nuage de points
Définition
Pour visualiser un éventuel lien entre deux variables $x$ et $y$, il suffit de tracer un nuage de points.
On considère une série statistiques à deux variables $x$ et $y$ pouvant prendre $n$ valeurs : $x_1$ à $x_n$ et $y_1$ à $y_n$.
Dans un repère orthogonal, le nuage de points représentant la série statistique est l'ensemble des $n$ points $M_i$ de coordonnées $(x_i;y_i)$.
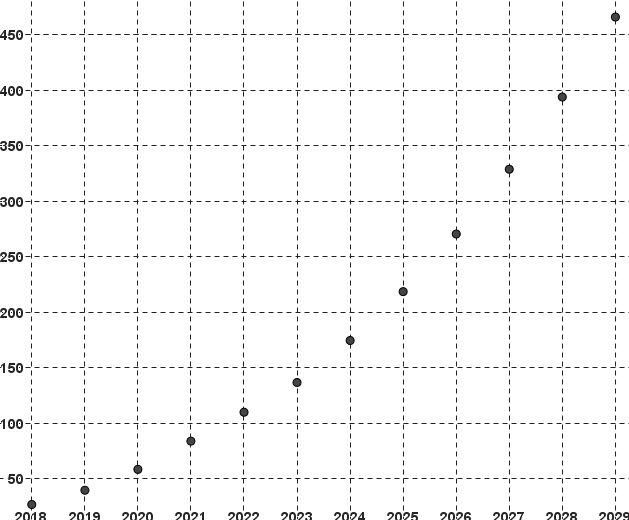
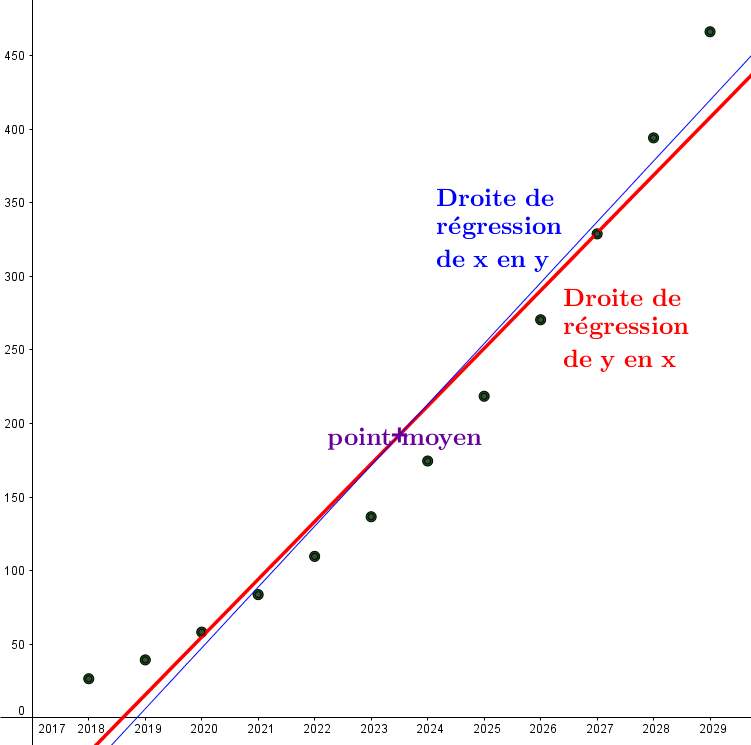
Le nuage de points associé à
la série statistique liant l'année au trafic mondial
de données sur le réseau mobile est :

L'année est en abscisse et le trafic en ordonnées (en Exaoctets).
Utilisation de Geogebra
Il est possible d'obtenir un nuage de points d'une statistiques à deux variables directement sur Geogebra. Pour cela, il suffit :
-
Ouvrir le Tableur de Geogebra :
-
Remplir le tableau avec les deux lignes correspondant aux données des deux variables.
-
Sélectionner l'ensemble des cases correspondant aux données.
-
Cliquer sur l'icône "Statistiques à deux variables" :
-
Cliquer sur le bouton "Analyse" : le nuage de points apparaît alors
Appliquons cette démarche sur les données du deuxième exemple.
-
On clique sur Tableur :

-
On remplit le tableau des données :

Plutôt que d'effectuer des copier-coller des tableaux des données du deuxième exemple, vous pouvez directement télécharger le contenu du fichier Geogebra avec le tableau rempli. -
Sélectionner toutes les cases de données (de A1 à AQ2) et cliquer sur l'icône
 .
.
-
On voit apparaître la fenêtre suivante :
Cliquer sur le bouton "Analyse". -
On voit apparaître le nuage de points suivant :
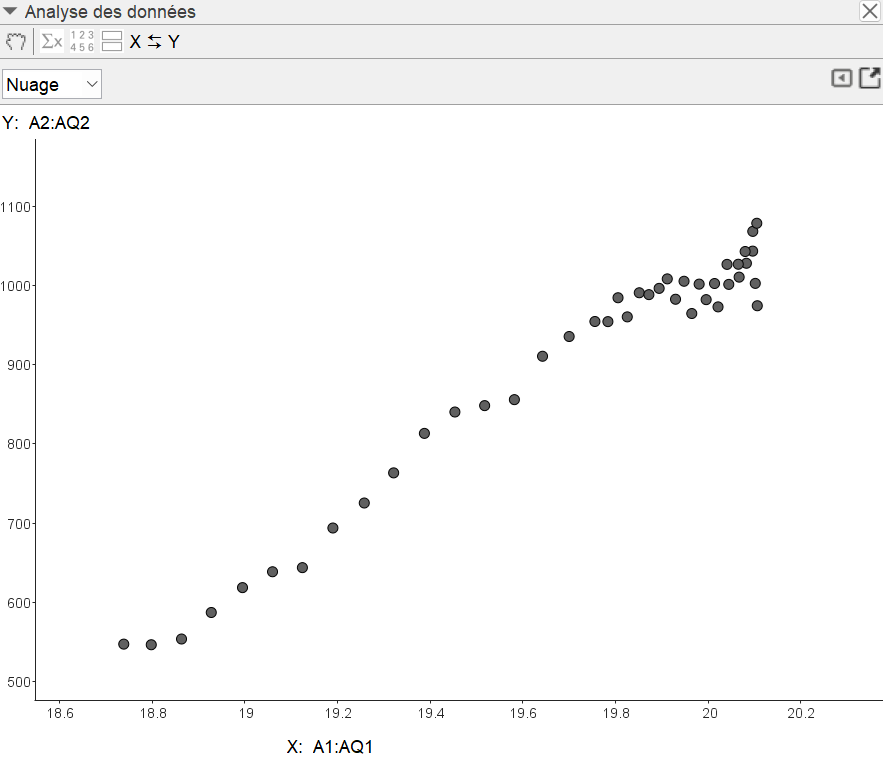
La distance Uranus-Lune est en abscisse (en Unité Astronomique), la production électrique japonaise de la même année est en ordonnée (en Giga kWh).
Un nuage de points d'une statistiques à deux variables n'est pas forcément un sous-ensemble d'une courbe représentant une fonction, car il peut y avoir deux points distincts avec la même abscisse.
-
Utilisez Geogebra afin d'obtenir le nuage de points associés aux données du troisième exemple.
-
Au vu de l'allure globale obtenue, quelle courbe géométrique simple permettrait d'approcher l'ensemble de tous les points ?
Un nuage de points permet d'avoir une vision globale des données d'une série statistiques
à deux variables.
Par contre, en statistiques, on préfère "résumer" une série avec quelques éléments.
Ainsi, l'idée désormais est de synthétiser une partie de l'information du nuage en un seul point,
puis voir ensuite comment synthétiser une information moins réduite du nuage par une droite,
ou une courbe représentant une fonction.
Ajustement affine par la méthode de Mayer
Point moyen
Le but ici est de synthétiser une partie de l'information du nuage en un seul point.
On considère une série statistiques à deux variables.
| Première variable $x$ | $x_1$ | $x_2$ | ... | $x_i$ | ... | $x_n$ |
|---|---|---|---|---|---|---|
| Seconde variable $y$ | $y_1$ | $y_2$ | ... | $y_i$ | ... | $y_n$ |
Le point moyen de cette série est le point $PM$
dont l'abscisse est la moyenne (arithmétique) des $n$ valeurs $x_i$ et
dont l'ordonnée est la moyenne (arithmétique) des $n$ valeurs $y_i$.
$PM\left(x_{PM};y_{PM}\right)$ avec
$x_{PM}=\displaystyle \dfrac{1}{n}\sum_{i=1}^{i=n}x_i=\dfrac{x_1+x_2+...+x_i+...+x_n}{n}$
et $y_{PM}=\displaystyle \dfrac{1}{n}\sum_{i=1}^{i=n}y_i=\dfrac{y_1+y_2+...+y_i+...+y_n}{n}$.
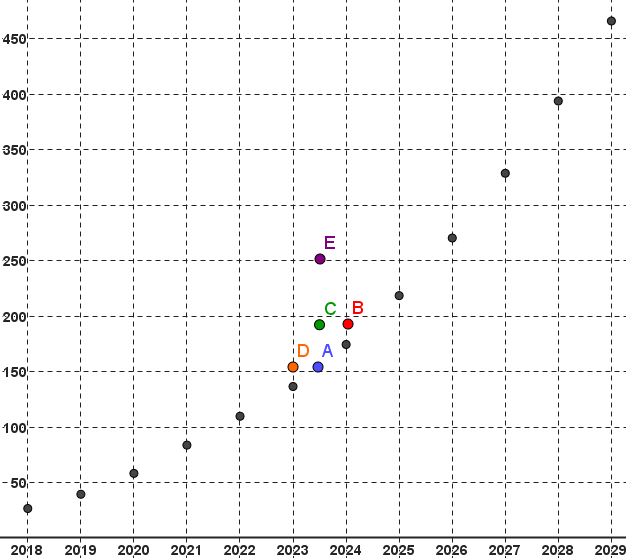
Parmi les 5 points colorés suivants, lequel correspond davantage au point moyen de la série statistique
à deux variables de l'exemple 1 ?
Sur Geogebra, pour faire apparaître le point moyen d'un nuage de points, il suffit :
-
Sélectionner toutes les valeurs de la série dans la partie Tableur.
-
Créer par clic droit
Liste de points:
-
Repérer dans la partie Algèbre le nom de la liste de points créé.
-
Pour créer le point moyen, saisir
PM=(MoyenneX(nom_liste_points),MoyenneY(nom_liste_points)).
Voici l'application de la méthode sur les données de l'exemple 2.
-
Pour obtenir dans la fenêtre Graphique, le nuage de points, il suffit de sélectionner les deux lignes de données déjà remplie dans le Tableur puis de cliquer sur "Créer" et "Liste de points" :
-
Pour voir apparaître le nuage il suffit de recadrer le graphique en faisant un clic gauche dans la zone du Graphique puis en cliquant sur "recadrer" :
Vous devez voir apparaître dans Graphique un nuage de points proche de celui-ci :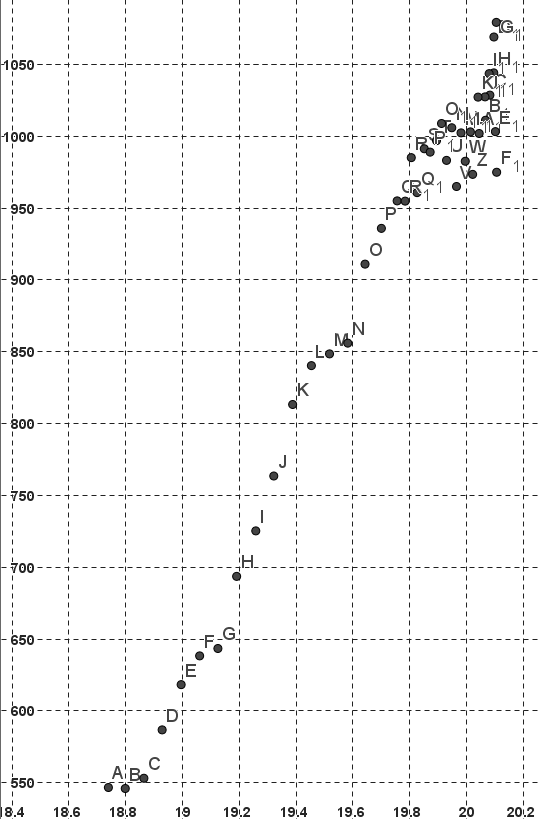
Si vous ne voulez pas voir le nom des points, il vous suffit d'ouvrir la partie Algèbre, puis de sélectionner tous les points (avec CTRL+A), faire un clic droit sur la sélection, enfin de cliquer sur "Afficher l'étiquette" afin d'enlever l'affichage de ces étiquettes :
Ainsi, vous aurez seulement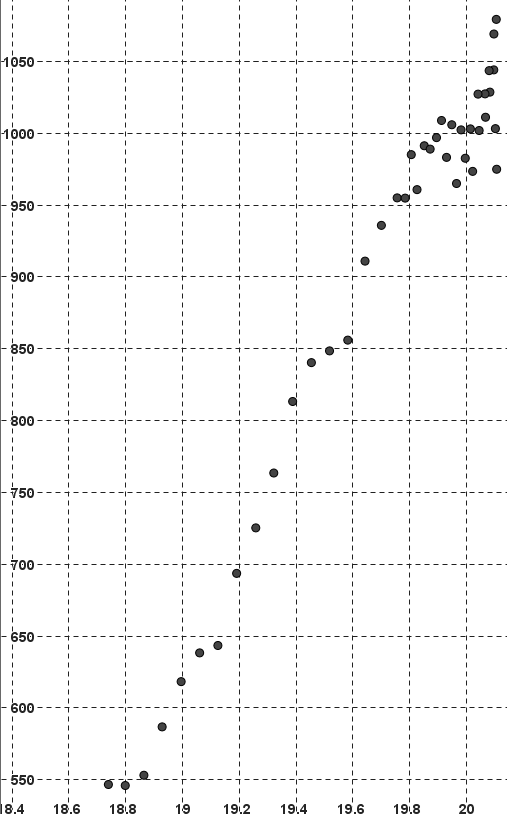
-
On voit apparaître la liste de points graphiquement et dans la partie Algèbre, normalement sous le nom de
l1: .
.
-
Créer le point moyen du nuage de points en tapant dans la zone de saisie :
PM=(MoyenneX(l1),MoyenneY(l1)).

Ce point moyen est visible désormais dans la partie Graphique et dans celle Algèbre où ses coordonnées approchées sont lisibles :
Ce point moyen signifie qu'en moyenne entre 1980 et 2021 la distance Lune-Uranus est d'environ $19.69$ unités astronomiques et qu'en moyenne entre 1980 et 2021 la production électrique du Japon fut d'environ $790.79$ milliards de kWh.
-
Créer le point moyen associé à la série statistique à deux variables issues de l'exemple 3.
-
Interpréter concrètement les deux coordonnées de ce point moyen.
Méthode de Mayer
Dans le cas où le nuage est allongé, il est plus pertinent de synthétiser une partie de l'information du nuage à l'aide d'une droite.
On considère le nuage de points de l'exemple 1 :
-
Parmi les droites ci-dessous, laquelle vous semble au mieux synthétiser le nuage de points ?
-
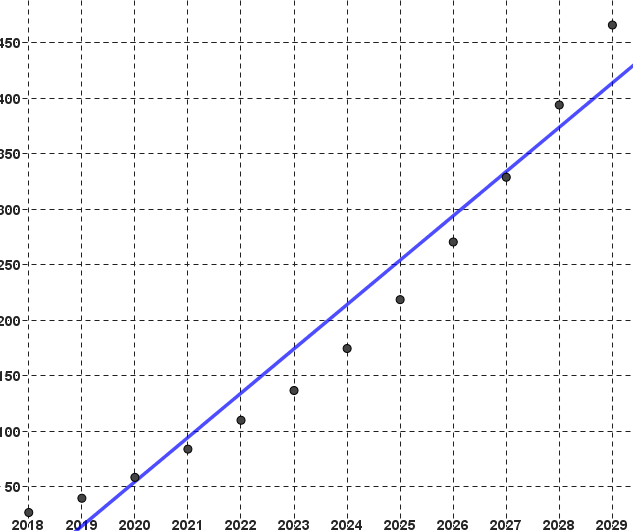
Droite 1 :
-
Droite 2 :
-
Droite 3 :
-
Droite 4 :
-
-
Si vous aviez à tracer à main levée une droite telle droite d'ajustement, c'est-à-dire qui "colle aux mieux" au nuage de points, quelle démarche naïve proposeriez-vous ?
Considérons une série statistique à deux variables dont le nuage de points
est allongé.
Coupons la série statistique en deux sous-séries de taille similaire.
Notons $PM_1$ le point moyen de la première série et $PM_2$ celui de la
deuxième série.
La droite $(PM_1PM_2)$ passant par les deux points moyens est appelée la droite de Mayer.
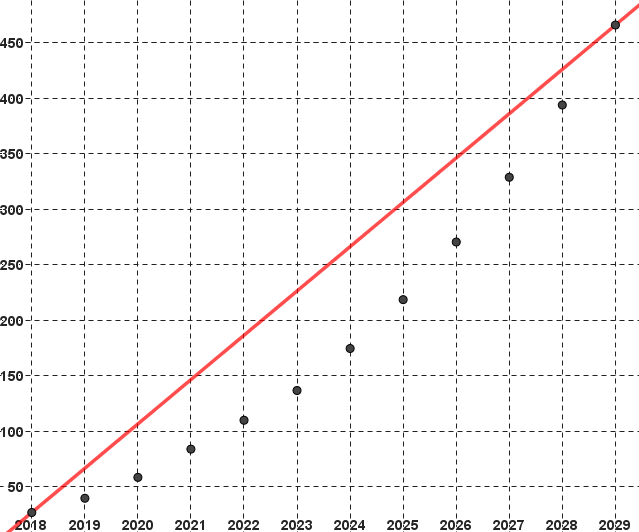
Reprenons les données de l'exemple 1.
En considérant comme première sous-série, les valeurs correspondant aux années comprises
entre 2018 et 2023, et comme seconde celles allant de 2024 à 2029, on obtient les deux
points moyens et la droite de Mayer ci-dessous :
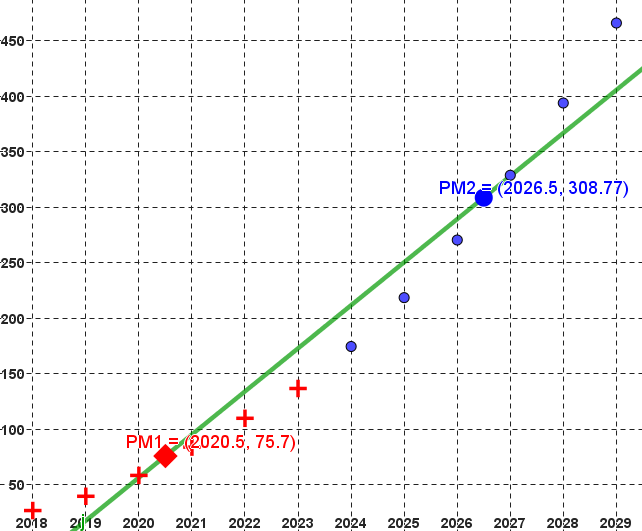
On admet que si le nuage de points est d'allure "allongée" alors la droite de Mayer constitue une "assez bonne" droite d'ajustement du nuage de points.
Pour obtenir sur Geogebra une droite de Mayer associée à une série statistiques à deux variables, il suffit de :
-
Créer une première
Liste de pointsà partir de la première moitié des valeurs sélectionnées dans la partie Tableur. -
Créer le point moyen de cette première moitié en utilisant les fonctions
MoyenneXetMoyenneYqui calculent la moyenne pour chacune des deux variables. -
Créer une seconde
Liste de pointsà partir de la seconde moitié des valeurs sélectionnées dans la partie Tableur. -
Créer le point moyen de cette deuxième moitié.
-
Créer la droite passant par ces deux points moyens.
Voici l'application de la méthode sur les données de l'exemple 2.
-
Sélectionner la première moitié des données (cases B1 à W2) puis en faire une nouvelle liste de points :
On la voit apparaître graphiquement et dans la partie Algèbre, normalement sous le nom del2: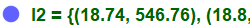
Sélectionner la seconde moitié des données (cases X1 à AQ2) puis en faire une nouvelle liste de points, qui sera normalement enregistrée sous le nom del3. -
Créer le point moyen de la première moitié du nuage de points en tapant dans la zone de saisie :
PM1=(MoyenneX(l2),MoyenneY(l2)).

Ce point moyen est visible désormais dans la partie Graphique et dans celle algèbre :
Créer le point moyen de la seconde moitié du nuage de points en tapant dans la zone de saisie :PM2=(MoyenneX(l3),MoyenneY(l3)):
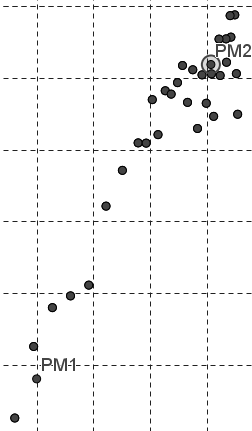
-
Cliquer sur l'onglet "Droite"
Puis sur les pointsPM1etPM2.
Alors, la droite de Mayer apparaît dans la zone Graphique :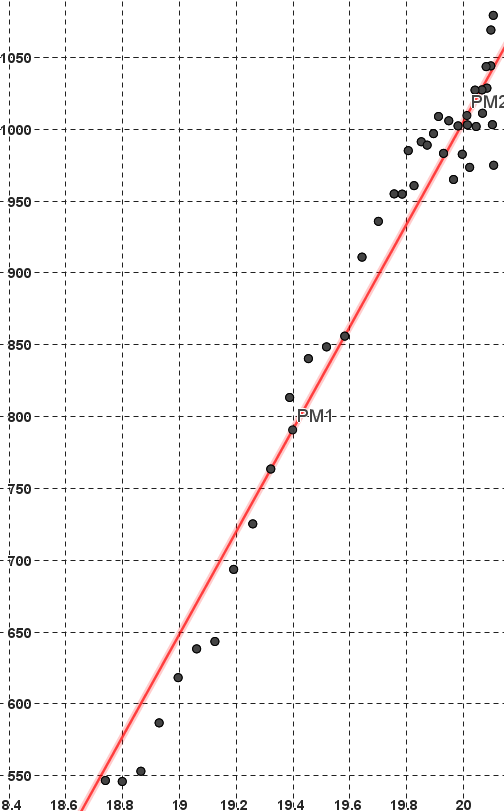
-
Utiliser Geogebra afin d'obtenir le nuage de points associés aux données du troisième exemple.
-
Tracer la droite de Mayer associée à ce nuage de points en faisant en sorte que le point moyen $PM_1$ portent sur les 5 premiers points.
Utilisation d'une droite de Mayer
Considérons une série statistique à deux variables.
Il est possible de conjecturer la valeur d'une variable connaissant la valeur d'une deuxième
en utilisant la droite de Mayer.
Attention, cela donne l'estimation d'une valeur possible, rien ne garantit la pertinence
réelle de cette valeur.
En utilisant la droite de Mayer résumant le nuage de points associé à
la série statistique liant l'année au trafic mondial
de données sur le réseau mobile, on peut estimer le trafic en 2030
a environ $447.73$ Exaoctets :
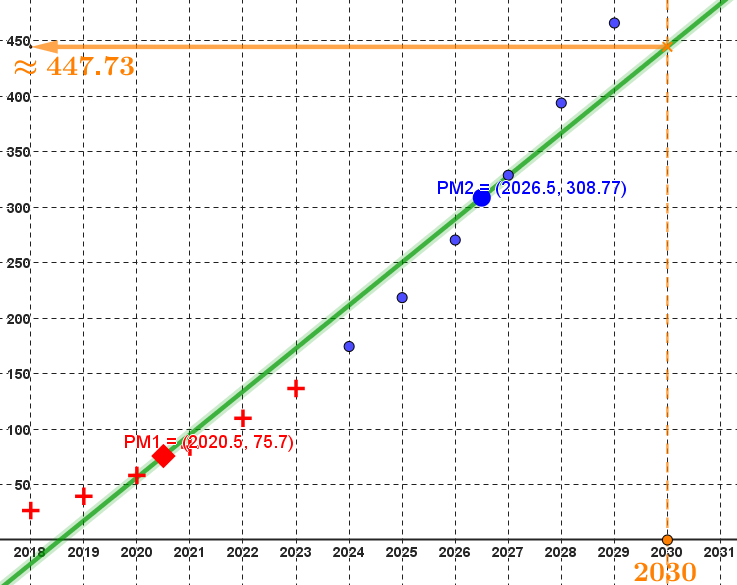
Cette estimation peut paraître ici peu pertinente du fait qu'elle est inférieure à la
valeur prévue pour 2029 et que le trafic mondial de données sur le réseau mobile ne fait que de croître.
Pour calculer à l'aide de la droite de Mayer la valeur d'une variable connaissant la valeur d'une deuxième valeur, il suffit :
-
Récupérer l'équation de la droite de Mayer obtenue sur Geogebra.
-
Remplacer dans cette équation l'inconnue de la variable dont on connaît la valeur par cette valeur.
-
Résoudre (à la main ou sur Xcas) cette équation pour obtenir la valeur de la seconde variable.
Appliquons cette démarche sur les données du
deuxième exemple.
D'après la production électrique totale du Japon en 2022
s'est élevé à $991.37$ milliards de kWh.
-
On fait apparaître dans la zone Algèbre l'équation de la droite de Mayer :

-
La production électrique apparaît en ordonnées sur le graphique donc il faut remplacer l'inconnue $y$ par la valeur connue de $991.37$ dans l'équation $-218.77x+0.61y=-3758.81$.
-
En résolvant sur Xcas, on peut estimer la distance moyenne entre Uranus et la Lune en 2022 :

Elle serait proche de 19.95 unités astronomiques.
Il est possible d'obtenir cette distance moyenne avec un programme python
en utilisant les modules astropy et jplephem.
Le code suivant permet d'importer plus de 100 Mo de données (au format .bsp) du
Jet Propulsion Laboratory
centre états-unien ayant entre en charge l'exploration spatiale puis de calculer la distance voulue en 2022.
from astropy.time import Time
from astropy.coordinates import get_body, solar_system_ephemeris
from astropy.coordinates import EarthLocation
# Date du premier jour de chaque mois de l'année 2022
dates = [f'2022-{mois:02d}-01' for mois in range(1, 13)]
# Position sur Terre (peu important dans les calculs en fait)
lieu_terre = EarthLocation.of_site('greenwich')
# Utilisation des éphémérides du Jet Propulsion Laboratory (JPL) pour pouvoir effectuer des calculs précis
with solar_system_ephemeris.set('jpl'):
# Conversion des dates des premiers du mois en objet de la classe Time
temps = Time(dates)
# Positions de la Lune et d'Uranus
positions_lune = get_body('moon', temps, lieu_terre)
positions_uranus = get_body('uranus', temps, lieu_terre)
# Calcul de la distance entre Uranus et la Lune
distances = positions_lune.separation_3d(positions_uranus)
# calcul de la moyenne en unités astronomiques puis son affichage arrondie à 10^(-4) près
moyenne = 0
for distance in distances:
moyenne += distance.au
print(f"La distance moyenne sur le premier jour de chaque mois de 2022 est d'environ {moyenne/12:.4f} unités astronomiques")
On obtient l'affichage suivant :
La distance moyenne sur le premier jour de chaque mois de 2022 est d'environ 19.7360 unités astronomiques.
L'erreur commise avec la valeur obtenue grâce à la droite de Mayer est environ de seulement 1% d'après le calcul
de pourcentage d'erreur relative : $\dfrac{\text{Valeur exacte}-\text{Valeur approchée}}{\text{Valeur exacte}}\times 100$ :

-
Reprendre la droite de Mayer de l'exercice précédent.
-
Lire dans la partie Algèbre (CTRL+MAJ+A) de Geogebra l'équation de la droite de Mayer.
-
D'après le bureau états-unien des statistiques sur le travail, il y avait 20680 personnes travaillant comme programmeur informatique en Californie en mai 2023.
En utilisant la droite de Mayer obtenue précédemment, estimer le nombre d'étudiant.e.s diplômé.e.s d'un Master en mathématiques et statistiques aux États-Unis en 2023.
Considérons une série statistiques à deux variables $x$ et $y$.
Pour une valeur $X$ de la variable $x$, la droite de Mayer permet de
"prévoir" la valeur correspondante $Y$ de la variable $y$.
-
Si $X$ apparient à l'intervalle d'observation de la série $x$, c'est-à-dire si $X$ est compris entre les valeurs extrêmes prises par $x$, alors on parle d'interpolation.
-
Si $X$ n'apparient à l'intervalle d'observation de la série $x$, c'est-à-dire si $X$ n'est compris entre les valeurs extrêmes prises par $x$, alors on parle d'extrapolation.
interpolation comme intérieur à l'intervalle d'observation.
extrapolation comme extérieur à l'intervalle d'observation.
Les mêmes définitions ont lieu si on "prévoit" $X$ à partir d'une valeur $Y$ de $y$.
-
Dans la prévision de l'exemple 6 permettant d'estimer le trafic mondial de données sur le réseau mobile en 2030, a-t-on affaire à une intrapolation ou une extrapolation ?
-
Dans la prévision de l'exemple 7 permettant d'estimer la distance Uranus-Lune en 2022, a-t-on affaire à une intrapolation ou une extrapolation ?
-
Dans l'exercice précédent permettant d'estimer le nombre d'étudiant.e.s diplômé.e.s d'un Master en mathématiques et statistiques aux États-Unis en 2023, a-t-on affaire à une intrapolation ou une extrapolation ?
Ajustement affine par la méthode des moindres carrés
Droites de régression
Le but est d'approcher "au mieux" le nuage de points par une droite : on parle d'ajustement affine.
Reste à définir le sens de "au mieux" !
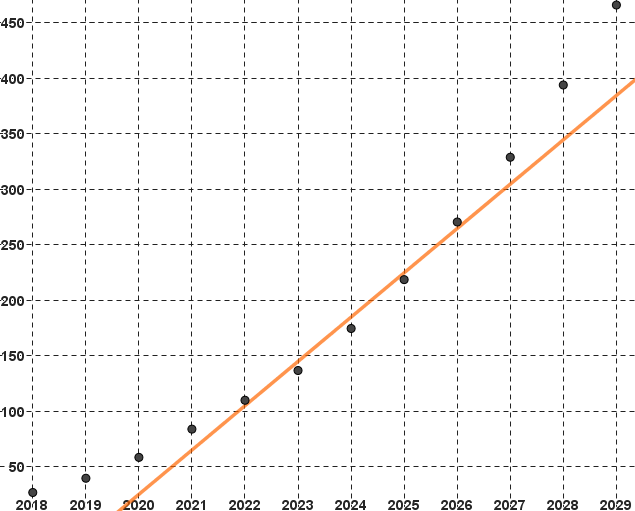
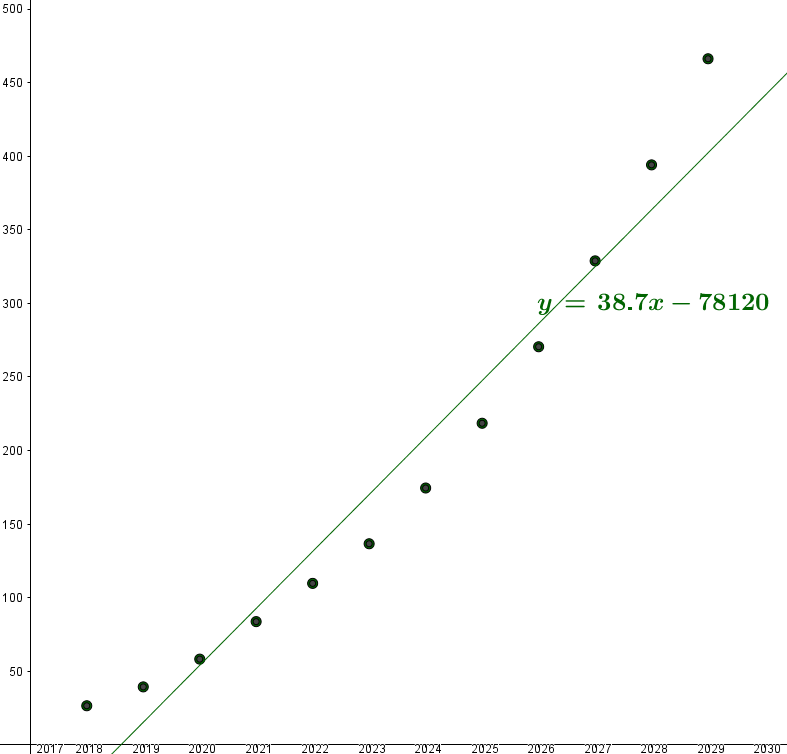
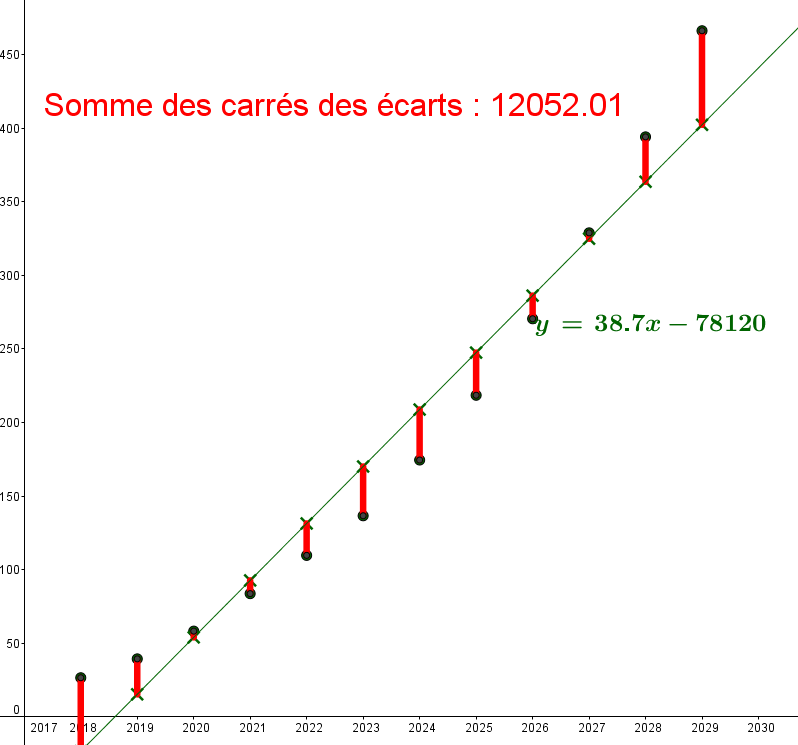
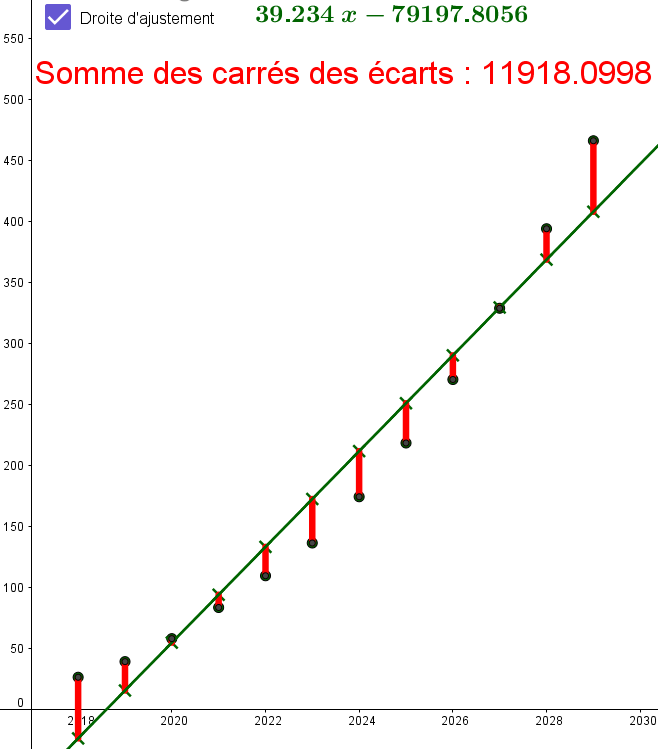
Reprenons les données de l'exemple 1.
La droite d'équation $y=38.7x-78120$ est une droite qui approche pas mal le nuage de points :
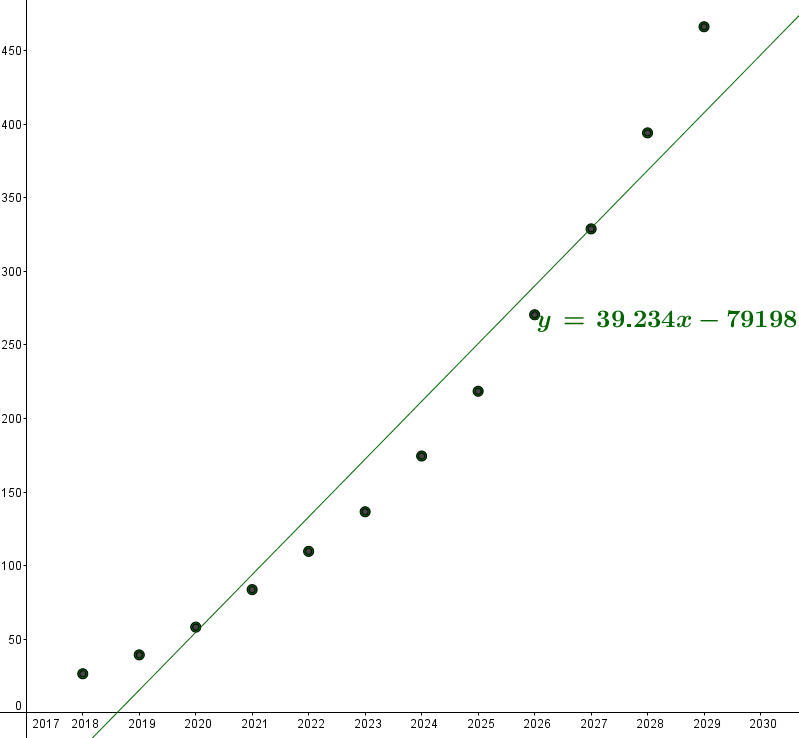
Tout comme la droite d'équation $y=39.234x-79198$ :
Comment déterminer laquelle des deux est préférable ?
On utilise pour cela la notion de moindres carrés.
Pour chacune des droites, on va calculer la somme des écarts au carré entre chaque point du
nuage avec le point de la droite ayant la même abscisse. Sur la figure, cela revient à
la somme des carrés des longueurs en rouge.
Pour la première droite la somme vaut environ : 12052 :
Pour la deuxième droite la somme vaut environ : 11919 :
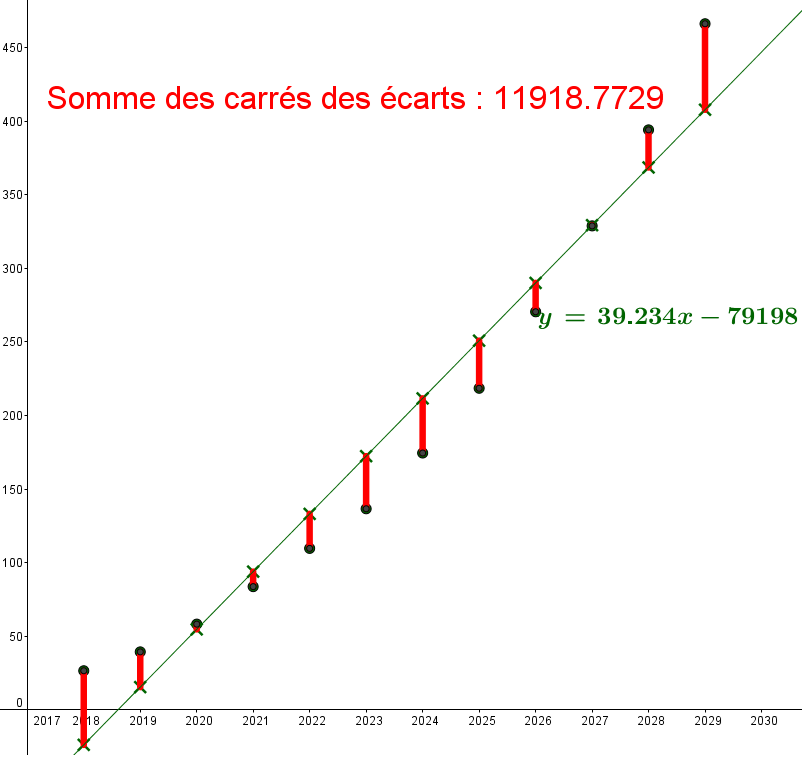
Au sens des moindres carrés, la seconde droite approche mieux
le nuage de points.
En déplaçant les curseur a et b du fichier Geogebra ci-dessous,
arrivez-vous à trouver une droite approchant mieux le nuage de points au sens des moindres carrés ?
On appelle droite de régression de $y$ en $x$ par la méthode des moindres carrés l'unique droite qui minimise la somme des carrés des écarts entre chaque point du nuage avec le point de la droite ayant même abscisse.
Il existe aussi une
droite de régression de $x$ en $y$ par la méthode des moindres carrés :
c'est l'unique droite qui minimise la somme des carrés des écarts entre chaque point du nuage
avec le point de la droite ayant même ordonnée :
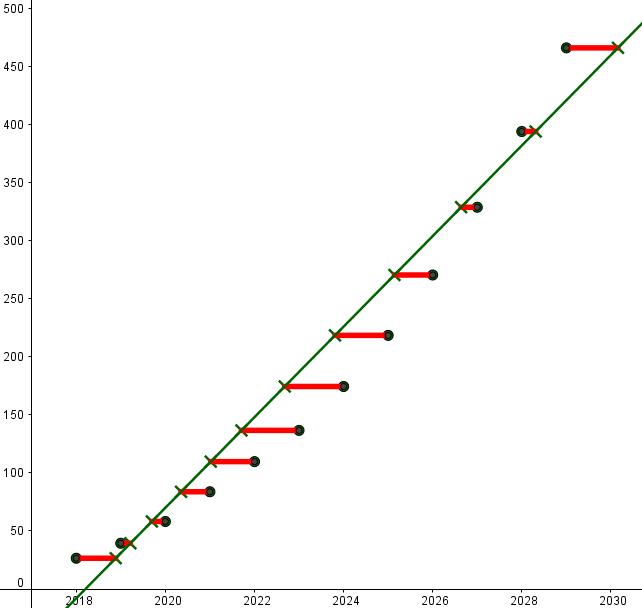
La droite de régression de $y$ en $x$ par la méthode des moindres carrés passe par le point moyen de la série statistique à deux variables.
Covariance d'une série statistique à deux variables
On considère une série statistique à deux variables $x$ et $y$.
On note $\overline{x}$ la moyenne des valeurs de la variables $x$
et $\overline{x}$ celle des valeurs de la variable $y$.
$\displaystyle \overline{x}=\dfrac{x_1+x_2+...+x_i+...+x_n}{n}=\dfrac{1}{n}\sum_{i=1}^{i=n}x_i$.
On appelle covariance de la série statistique à deux variables
le nombre $cov(x,y)$ défini par la formule suivante :
$cov(x,y)=\dfrac{(x_1-\overline{x})(y_1-\overline{y})+(x_2-\overline{x})(y_2-\overline{y})+...+(x_i-\overline{x})(y_i-\overline{y})+...+(x_n-\overline{x})(y_n-\overline{y})}{n}$,
soit $cov(x,y)=\displaystyle\dfrac{1}{n}\sum_{i=1}^{i=n}(x_i-\overline{x})(y_i-\overline{y})$.
On note aussi ce nombre $cov(x,y)$ sous la forme $\sigma_{xy}$.
On peut calculer la covariance par la formule suivante : $cov(x,y)=\displaystyle\dfrac{(x_1\times y_2)+(x_2\times y_2)+...+(x_i\times y_i)+...+(x_n\times y_n)}{n}-\overline{x}\times\overline{y}$, soit $cov(x;y)=\displaystyle\dfrac{1}{n}\sum_{i=1}^{i=n}x_i\times y_i-\overline{x}\times\overline{y}$.
La formule de la variance de la variable aléatoire $x$ est donnée par la formule :
$V(x)=\displaystyle\dfrac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+...+(x_i-\overline{x})^2+...+(x_n-\overline{x})^2}{n}$, soit
$V(x)=\displaystyle\dfrac{1}{n}\sum_{i=1}^{i=n}(x_i-\overline{x})^2$.
En remplaçant $y$ par $x$, on voit bien l'analogie entre la variance d'une variable $x$ et
la covariance de deux variables $x$ et $y$.
Plutôt que de calculer à la main la covariance, il est possible de l'obtenir directement sur Geogebra.
Supposons qu'une série statistique à deux variables est déjà stockée dans Geogebra sous la forme
d'une liste de points l1.
Pour obtenir la covariance $cov(x,y)$, il suffit de saisir Covariance(l1).
Pour l'exemple 1, Covariance(l1) conduit à la valeur :
$cov(x,y)\approx 467.54$. 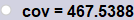
Déterminer la covariance de la série statistique correspondant à l' exemple 2.
Équation des droites de régression
Soit une série statistique à deux variables $x$ et $y$ de covariance $cov(x,y)$ et dont la variable $x$ a pour moyenne $\overline{x}$ et pour variance $V(x)$, et dont la variable $y$ a pour moyenne $\overline{y}$ et pour variance $V(y)$.
La droite de régression de $y$ en $x$ possède une équation réduite de la forme $y=ax+b$ où le coefficient directeur $a=\dfrac{cov(x,y)}{V(x)}$ et où $b$ vérifie l'équation $\overline{y}=a\overline{x}+b$, puisque cette droite de régression passe par le point moyen.
La droite de régression de $x$ en $y$ possède une équation réduite de la forme $x=a'y+b'$ où le coefficient directeur $a'=\dfrac{cov(x,y)}{V(y)}$ et où $b'$ vérifie l'équation $\overline{x}=a'\overline{y}+b'$, puisque cette droite de régression passe par le point moyen.
-
Sur Geogebra, l'instruction
nVarXprend en paramètre une liste de points et renvoie la valeur $n\times V(x)$.
De même, l'instructionnVarYprend en paramètre une liste de points et renvoie la valeur $n\times V(y)$. -
Sur Geogebra, l'instruction
nCovprend en paramètre une liste de points et renvoie la valeur $n\times cov(x,y)$.
On reprend l'exemple 1.
Le but est de déterminer l'équation de la droite de régression $\mathcal{D}$ de $y$ en $x$ de cette série.
-
Calculer la valeur du coefficient directeur $a$ de la droite de régression $\mathcal{D}$.
-
Vérifier que cette valeur est très proche de $39.234$, valeur conjecturée à l'exemple 8 et dans l'exercice 8.
-
En utilisant le fait que cette droite de régression passe par le point moyen, déterminer une équation dont l'ordonnée à l'origine $b$ est solution.
-
Calculer la valeur de l'ordonnée à l'origine $b$ de la droite de régression $\mathcal{D}$.
-
Vérifier que cette valeur est très proche de $-79198$, valeur conjecturée à l'exemple 8 et dans l'exercice 8.
Droite de régression sur Geogebra
Plutôt que d'effectuer le calcul de l'équation de la droite de régression,
il est possible d'obtenir directement cette équation et le tracé de la droite
de régression sur Geogebra.
Ceci est fondamental à savoir faire pour le BTS CIEL.
Pour obtenir la droite de régression d'une série statistique à deux variables, il suffit :
-
De saisir les données dans la partie Tableur de Geogebra.
-
De sélectionner l'ensemble des données.
-
De cliquer ensuite sur l'icône "Statistiques à deux variables" :
-
De cliquer sur le bouton "Analyse".
-
De choisir "Linéaire" come modèle d'ajustement :

Voici comment obtenir sur Geogebra directement la droite de régression de $y$ en $x$ pour la série statistique de l'exemple 1 :
-
Saisir et sélectionner les données :

-
Après avoir cliqué sur "Statistiques à deux variables", apparaît l'écran suivant :
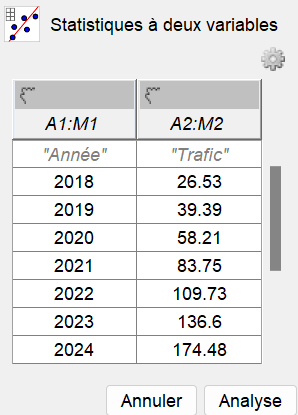
-
Après avoir cliqué sur "Analyse", apparaît l'affichage suivant :
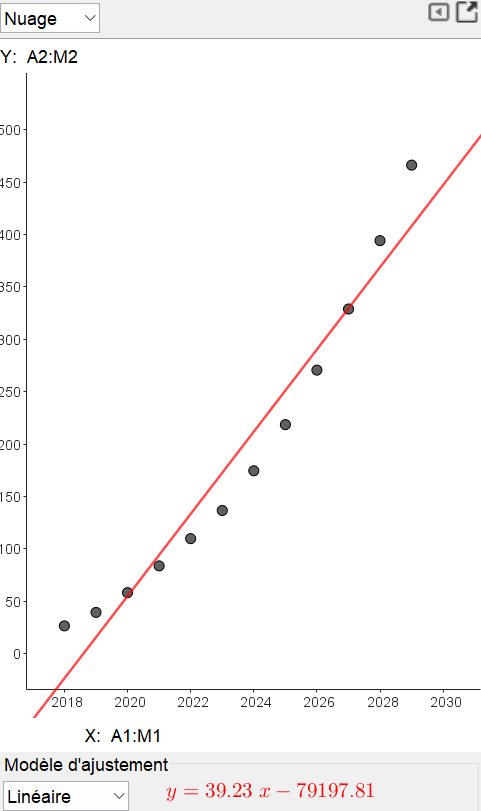
-
Éventuellement après avoir amélioré la précision de l'arrondi dans :
On peut alors lire l'équation de la droite de régression :
-
Suivre la démarche de l'exemple précédente afin d'obtenir l'équation de la droite de régression avec une précision de 10 décimales.
-
Utiliser la zone
 ,
pour obtenir une estimation du trafic mondial de données transitant sur le réseau mobile en Exaoctets en 2030.
,
pour obtenir une estimation du trafic mondial de données transitant sur le réseau mobile en Exaoctets en 2030.
-
Que pensez-vous de la pertinence de cette estimation ?
On reprend la série statistique de l'exemple 2.
-
Déterminer la droite de régression de $y$ en $x$ de la série statistique correspondant à l'exemple 2, avec des coefficients arrondis à $10^{-3}$ près.
-
On peut estimer grâce à un programme Python utilisant astropy que la distance moyenne entre Uranus et la Lune en 2022 est proche de $19.736$ unités astronomiques.
En utilisant la droite de régression, quelle estimation de la production électrique japonaise pouvez-vous donner ?
-
Déterminer la droite de régression de $x$ en $y$ de la série statistique correspondant à l'exemple 3.
Utiliser l'icône
 pour passer d'une régression de $y$ en $x$ à une régression de $x$ en $y$.
pour passer d'une régression de $y$ en $x$ à une régression de $x$ en $y$.
-
D'après le bureau états-unien des statistiques sur le travail, il y avait 20680 personnes travaillant comme programmeur informatique en Californie en mai 2023.
En utilisant la droite de régression de $x$ en $y$ obtenue précédemment, estimer le nombre d'étudiant.e.s diplômé.e.s d'un Master en mathématiques et statistiques aux États-Unis en 2023. -
Comparer la valeur obtenue avec l'estimation obtenue dans cet exercice avec la droite de Mayer.
Coefficient de corrélation linéaire et interprétation graphique
Nous avons obtenu pour différents problèmes des droites de regression, droites
qui nous ont permit d'effectuer des interpolations ou des extrapolations.
Cependant certaines estimations obtenues nous ont paru comme peu pertinentes.
Dès lors, comment estimer la pertinence de l'approximation d'une série statistique
par une droite de régression ?
C'est le but de cette partie ! En utilisant le coefficient de corrélation linéaire.
Le coefficient de corrélation linéaire d'une série statistique à deux variables $x$ et $y$ est le nombre noté souvent $r$, nombre défini par $r=\dfrac{cov(x,y)}{\sigma(x)\times \sigma(y)}$, où $cov(x,y)$ est la covariance des séries $x$ et $y$, $\sigma(x)$ est l'écart-type de la série $x$ et $\sigma(y)$ celui de la série $y$.
-
$r$ est toujours compris entre -1 et 1.
-
$r$ est toujours du signe de $cov(x,y)$.
Sur Geogebra, il est possible d'obtenir directement la valeur du coefficient de correlation linéaire
en cliquant sur l'onglet ![]() de l'affichage
de l'affichage
 .
.
Pour la série statistique de l'exemple 1, en cliquant
sur cet icône on obtient la fenêtre suivante :
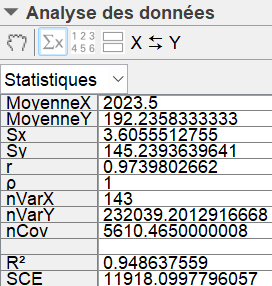
Ainsi, pour cette série, le coefficient de corrélation linéaire vaut environ $0.974$.
Le coefficient de corrélation linéaire est lié au coefficient directeur $a$ de
la droite de regression de $y$ en $x$ et à $\dfrac{1}{a'}$ où $a'$ est le coefficient
directeur de la droite de regression de $x$ en $y$.
Comme ces deux droites de régression passent toutes deux par le point moyen $(\overline{x};\overline{y})$,
$r$ donne une indication quant à l'angle formé entre ces deux droites.
-
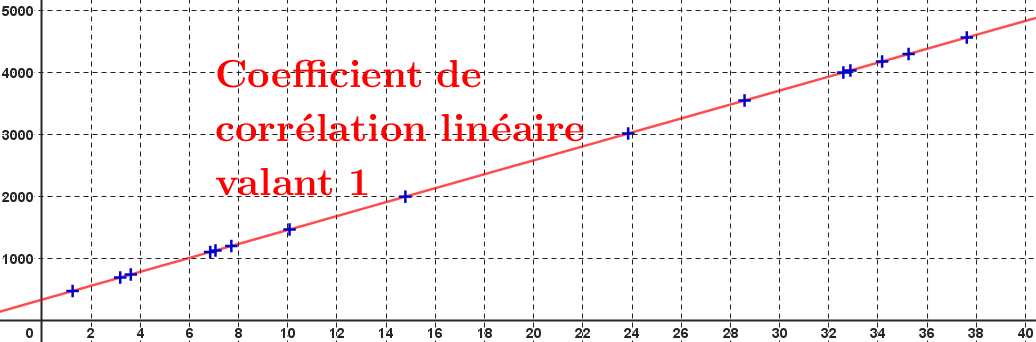
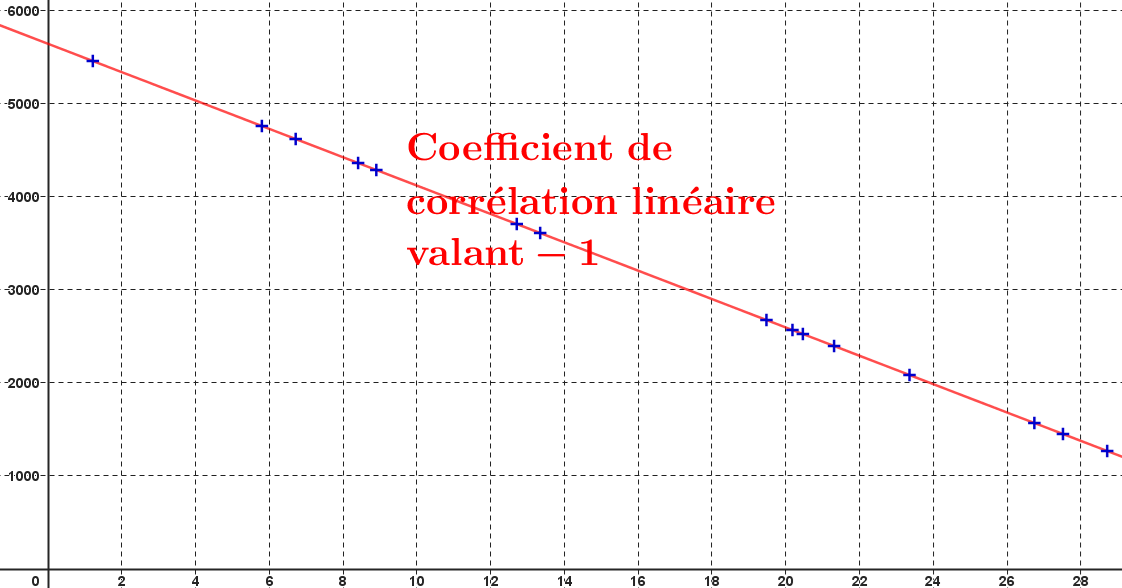
Si $r=1$ ou $r=-1$, alors l'angle est nul, si bien que les deux droites de régression sont confondues ; l'ajustement affine est "parfait" : tous les points du nuage sont alignés.
-
Cas où $r=1$ :
-
Cas où $r=-1$ :
-
-
Si $r$ est proche de 1 ou de -1 alors les deux droites de régression sont proches : on dit qu'il y a une "bonne" corrélation entre les deux variables.
Par exemple, la série statistiques à deux variables de l'exemple 1 a un coefficient de corrélation linéaire porche de 1 car l'angle entre les deux droites de régression est faible :
-
Si $r$ est proche de 0 alors les variables ne sont pas réellement corrélées.
Lorsque le coefficient de correlation linéaire est proche de 1 ou de -1, les deux variables sont dites fortement corrélées.
Déterminer le coefficient de correlation de la série statistique à deux variables associée à l'exemple 2.
Déterminer le coefficient de correlation de la série statistique à deux variables associée à l'exemple 3.
Il est fondamental en tant que citoyen.ne de comprendre qu'une forte correlation n'implique pas forcément un lien de causalité !
Comme exemple de cette différence, il suffit de considérer la production électrique
japonaise avec la distance moyenne Uranus-Lune.
La corrélation est très forte puisque $r$ est très proche de 1 puisque vaut $0.985$.
Pourtant, il n'y a évidemment aucun lien de cause à effet entre ces deux variables.
L'exemple 2 a été choisi pour ce cours aussi parce qu'il vérifie aussi une autre
caractéristique mathématique (hors programme) qui habituellement sert à justifier
que le résultat est statistiquement significatif
(valeur p inférieure à 0.01).
Cette valeur p si basse tendrait à penser qu'il est presque improbable de trouver au hasard des résultats
aussi corrélés.
Sauf que pour obtenir cet exemple, il a suffit de traiter un très grands nombres de données
publiques naturellement non en lien. Le hasard fait que certaines d'entre elles se voient être
fortement corrélées alors que pour la plupart $r$ est proche de 0 et la valeur p n'est pas significative.
Garder un cas rare parmi un très grand ensemble de cas réels en ne prenant pas en compte les
autres autres cas pourrait permettre de faire croire à un lien caché farfelu.
La production de tout autre pays que la Japon et sur une plage d'années différentes avec d'autres distances astronomiques
conduit à des coefficients de corrélations linéaires bien plus proches de 0.
Il est même possible de demander à une Intelligence Artificielle d'écrire un article de recherche
sur ce lien entre production électrique japonaise et la distance Uranus-Lune.
Voici un tel article qui n'a évidemment aucune valeur scientifique !
Ainsi, méfiez-vous des termes statistiquement significatifs qui dénote une corrélation
statistique et en aucun cas une preuve scientifique d'un lien de causalité !
Ajustement non affine
Nous avons vu avec l'exemple 1 qu'aucune des droites trouvées n'approche correctement
le nuage de points pour effectuer des estimations pertinentes.
Plutôt que d'approcher par une droite, l'idée est de désormais approcher le nuage de points par
une courbe représentant une fonction.
On considère une série statistique à deux variables :
| Première variable $x$ | $x_1$ | $x_2$ | ... | $x_i$ | ... | $x_n$ |
|---|---|---|---|---|---|---|
| Seconde variable $y$ | $y_1$ | $y_2$ | ... | $y_i$ | ... | $y_n$ |
Effectuer un ajustement de la seconde variable $y$ par la
variable $x$ revient à trouver une fonction $f$ telle que la courbe d'équation $y=f(x)$
passe "au plus près" du nuage de points.
Lorsque la fonction $f$ est une fonction affine, on parle d'ajustement affine.
Lorsque la fonction $f$ n'est pas une fonction affine, on parle d'ajustement non affine.
Vu l'allure du nuage de points associé à la série statistique de l'exemple 1,
il peut être intéressant d'essayer d'approcher le nuage par une fonction en lien avec la fonction exponentielle.
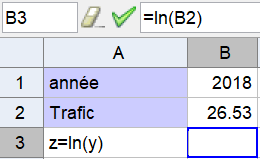
Ainsi, on procède au changement de variable $z=\ln(y)$.
Dans la cellule B3 du Tableur de Geogebra, il suffit de saisir =ln(B2) :
On reproduit la formule par glissement par la droite :

On copie-colle les lignes 1 et 3 au niveau des lignes 5 et 6 afin d'avoir
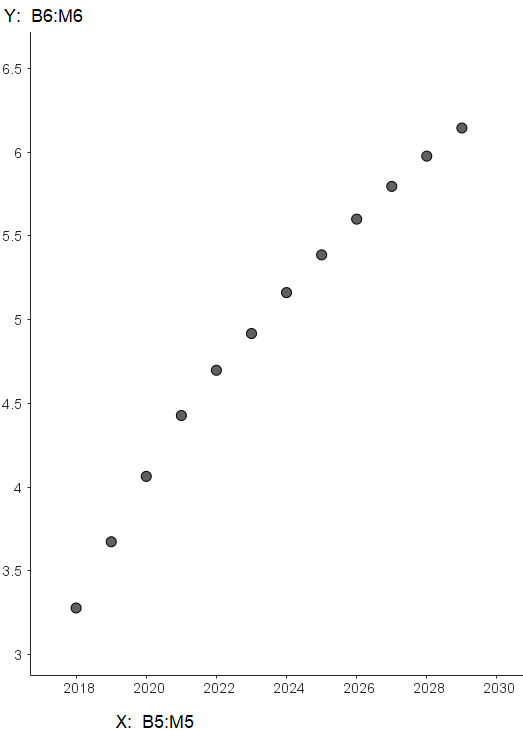
un tableau de deux lignes contiguës pour la série statistique à deux variables $x$ et $z$ :

On obtient pour cette série modifiée le nuage suivant :
-
Reproduire l'exemple précédent.
-
Déterminer le coefficient de corrélation linéaire associé à la série statistique à deux variables $x$ et $z$.
-
Avec la série de variables $x$ et $y$, le coefficient de corrélation linéaire est d'environ $0.974$.
Le changement de variable est-il pertinent ? -
Déterminer l'équation de la droite de régression de $z$ en $x$.
-
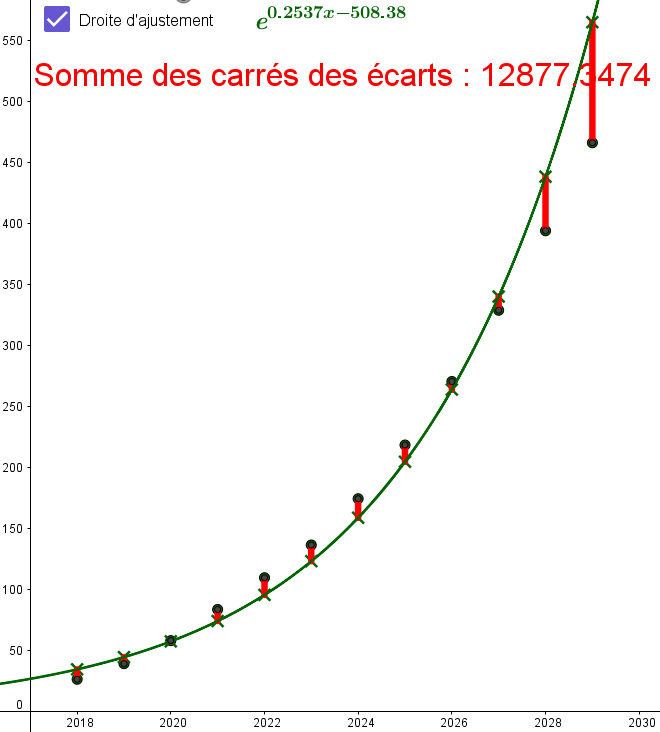
En déduire que la courbe représentant la fonction $g:x\mapsto \exp(0.25368 x -508.3859)$ approche à peu près le nuage de points.
Même si le coefficient de correlation linéaire est meilleure pour la régression de $z$ en $x$
par rapport à celle de $y$ en $x$, la somme des écarts des carrés est moins bonne pour la courbe
obtenue avec le changement de variable en $z$ :
Il est possible d'obtenir différents ajustements sur Geogebra pour une série statistique donnée :
-
Tester les différents ajustements sur Geogebra pour la même série statistique issue de l'exemple 1.
-
Quel ajustement trouvez-vous préférable ?
À l'aide de deux changements de variables, nous allons trouver une courbe approchant très bien le nuage de points de l'exemple 1.
-
Premier changement de variable : travailler avec le nombre d'années écoulées depuis 2018, plutôt qu'avec l'année.
Ce changement de variable revient à $x'=x-2018$.
Dans la ligne 8 du Tableur de Geogebra, faire apparaître la première ligne du tableau suivant :$x'$ années écoulées depuis 2018 0 1 2 3 4 5 6 7 8 9 10 11 $v=$ $\ln\left(\dfrac{900}{y}-1\right)$ ... ... ... ... ... ... ... ... ... ... ... ... -
Pour la seconde variable, on effectue le changement de variable suivant : $v=\ln\left(\dfrac{900}{y}-1\right)$.
Dans la ligne 9 du Tableur de Geogebra, compléter la seconde ligne du tableau ci-dessus en saisissant dans la cellule B9 la formule=ln(900 / B2 - 1)puis en la reproduisant par glissement. -
Obtenir le nuage de points associé aux deux variables $x'$ et $v$.
Le nuage est-il bien allongé ? -
Déterminer le coefficient de corrélation linéaire de la série statistique $(x';v)$.
Interpréter le résultat. -
Déterminer l'équation de la droite de régression de $v$ en $x'$.
-
En s'aidant du changement de variable $v=\ln\left(\dfrac{900}{y}-1\right)$, déduire que $\dfrac{900}{y}-1\approx 28 e^{-0.3131 x'}$.
-
En déduire que $y\approx \dfrac{900}{1+28 e^{-0.3131 (x-2018)}}$.
Le modèle permettant d'approcher $y$ à partir de $x$ grâce aux changements de variables
est appelé modèle logistique.
La somme des carrés des écarts est alors bien meilleur que celle obtenue par l'ajustement affine.
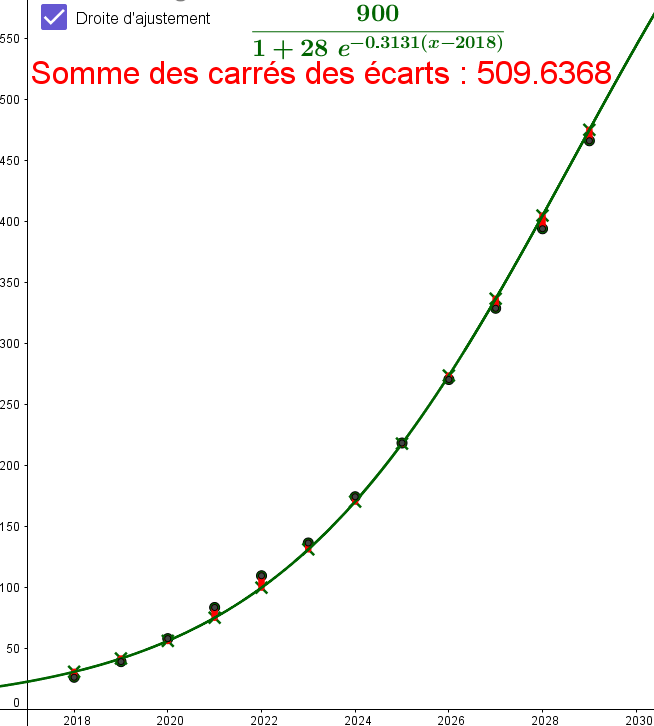

Geogebra n'a pas réussi à trouver directement cet ajustement logistique : vous êtes
meilleur.e.s que le logiciel ! Félicitations !
Voici un test de huit questions portant sur les statistiques à deux variables.
Les premières nécessitent surtout d'utiliser Geogebra et le cours.
Pour la dernière, le changement de variable nécessitera dans calculs posés sur une feuille.
Exercices
Les exercices suivants sont inspirés de sujets de BTS.
Les réussir est important pour le CCF de fin d'année.
Une société conçoit et commercialise un jeu vidéo d'aventure.
Ce jeu est constitué de plusieurs niveaux. Un joueur
débute au niveau 1 et peut passer au niveau supérieur en gagnant des points d'expérience.
Pour tout entier naturel $n$, non nul, on note $X_n$ le nombre de points d'expérience nécessaires
(en milliers) pour passer du niveau $n$ au niveau $n + 1$.
Le tableau ci-dessous indique, pour quelques niveaux, le nombre de points d'expérience
nécessaires (en milliers) pour passer au niveau suivant :
| Niveau $n$ | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|
| Nombre de points d'expérience nécessaires (en milliers) pour passer du niveau $n$ au niveau $n+1$ | 220 | 256 | 283 | 304 | 321 |
-
Déterminer le coefficient de corrélation linéaire $r$ de la série statistique $(n ; X_n )$. Arrondir le résultat au dixième et interpréter concrètement le résultat.
-
Déterminer une équation de la droite de régression de $X_n$ en $n$, sous la forme $X_n = a\times n + b$.
-
À l'aide de l'équation de la droite de régression trouvée précédemment, estimer le nombre de points d'expérience nécessaires pour passer du niveau 20 au niveau 21. Arrondir le résultat à 1 près.
-
Déterminer le premier niveau à partir duquel au moins 500 points d'expérience sont nécessaires pour passer au niveau suivant.
Une société commercialise des liseuses.
Le tableau ci-dessous, où $x_i$ désigne le rang de l'année mesuré à partir de
l'année 2015, donne le nombre $y_i$ de liseuses de cette marque vendues
annuellement depuis 2015.
| Année | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
|---|---|---|---|---|---|---|---|
| Rang de l'année $x_i$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Nombre $y_i$ de liseuses vendues | 1245 | 1320 | 1421 | 1480 | 1530 | 1680 | 1710 |
-
-
Déterminer le coefficient de corrélation linéaire $r$ de la série statistique $(x_i ; y_i)$. Arrondir le résultat au centième.
-
Expliquer pourquoi le résultat obtenu permet d'envisager un ajustement affine.
-
-
Déterminer une équation de la droite de régression de $y$ en $x$, sous la forme $y = ax + b$. Les coefficients $a$ et $b$ seront arrondis au dixième.
-
-
À l'aide de l'équation de la droite de régression trouvée précédemment, estimer le nombre de liseuses vendues en 2025.
-
À l'aide de l'équation de la droite de régression trouvée précédemment, estimer le rang de l'année à partir duquel le nombre de liseuses vendues deviendrait supérieur à 3 000.
-
Le glaucome est une maladie dégénérative du nerf optique qui entraîne une perte progressive de la vision. Cette maladie entraîne la dégénérescence des fibres nerveuses chargées de transmettre au cerveau les informations issues de la rétine.
La technique d’imagerie Tomographie en Cohérence Optique (OCT) permet de scanner la rétine et le nerf optique : en mesurant l’épaisseur des fibres du nerf optique on peut en déduire le nombre de fibres nerveuses optiques d’une personne.
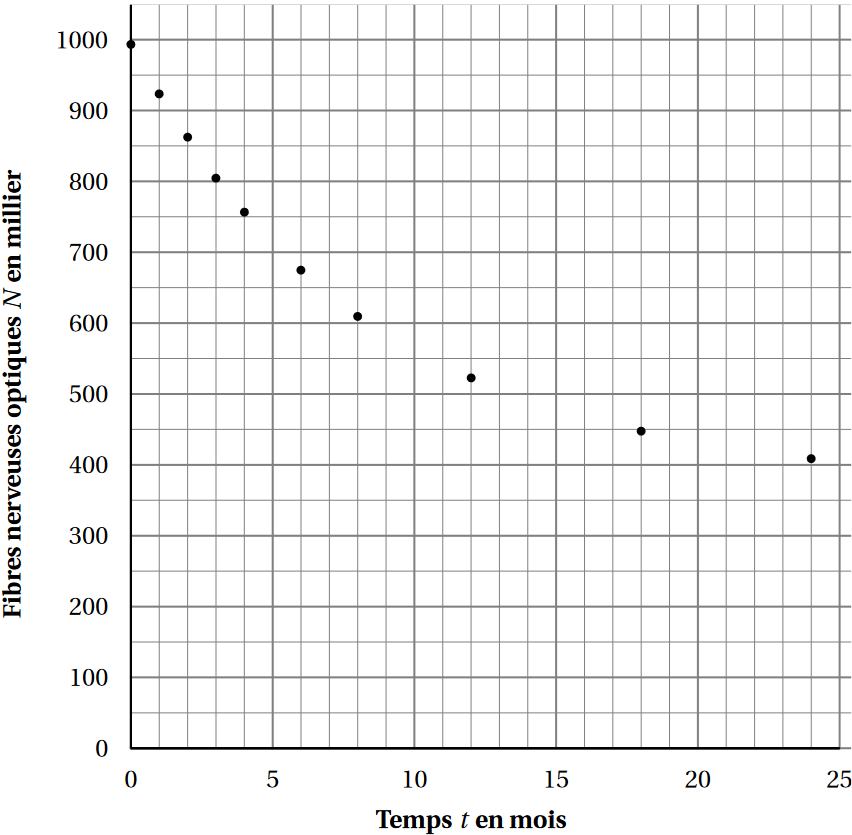
On a mesuré l’évolution du nombre $N$ de fibres nerveuses optiques, en millier,
en fonction du temps $t$ , exprimé en mois, d’une personne atteinte d’un glaucome aigu.
L’instant $t = 0$ représente le moment d’apparition du glaucome aigu.
On obtient les résultats suivants :
| Temps $t$ (en mois) | 0 | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 18 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|
| Fibres nerveuses optiques $N$ (en millier) | 994 | 924 | 863 | 805 | 757 | 675 | 610 | 523 | 448 | 409 |
-
-
À l’aide du graphique expliquer pourquoi un ajustement affine de $N$ en $t$ ne semble pas approprié.
-
Quel calcul permet de vérifier la non pertinence d'un ajustement affine dans ce cas ? Faire le calcul sur Geogebra.
-
-
-
Déterminer le coefficient de corrélation linéaire associé à cette série statistique $(t ; z)$.
-
Comparer les coefficients de corrélation linéaire des séries $(t ; N)$ et $(t ; z)$ et préciser pour quelle série un ajustement affine est-il le plus pertinent.
-
Donner, à l’aide de Geogebra, une équation de la droite de régression de $z$ en $t$ selon la méthode des moindres carrés, sous la forme : $z = at + b$, où $a$ et $b$ seront arrondis au millième.
-
En déduire une expression de $N$ en fonction de $t$ de la forme : $N = A e^{-0.12t} + 375$, où $A$ sera arrondi à l’unité.
-
En utilisant l'ajustement de la question précédente, pouvez-vous savoir si à très long terme le glaucome va détruire l'ensemble des fibres du nerf optique ?
-
Que pouvez-vous dire quant à la pertinence d'utiliser l'ajustement obtenu pour une extrapolation à très long terme ?
On décide de procéder à un changement de variable, en posant : $z=\ln(N-375)$.
On obtient alors le tableau de valeurs suivant (les résultats ont été arrondis à $10^{-2}$).Temps $t$ (en mois) 0 1 2 3 4 6 8 12 18 24 $z$ 6.43 6.31 6.19 6.06 5.95 5.70 5.46 5.00 4.29 3.53 -
Pour fabriquer des montures, on chauffe un matériau à 150 °C puis on le sort du four et on le laisse refroidir à température ambiante (28 °C).
Pour étudier le refroidissement du matériau, on a réalisé des relevés de température et réalisé
un croquis.
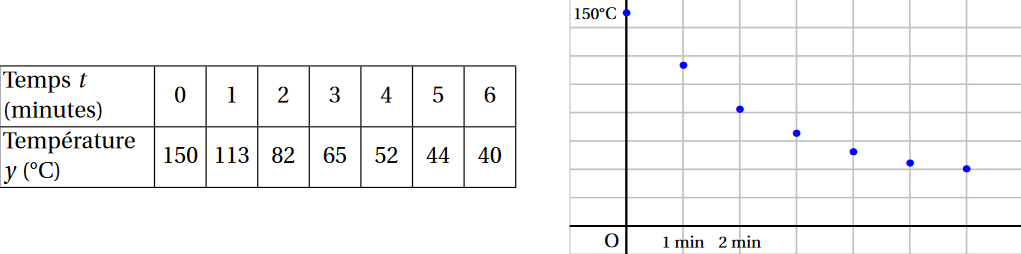
-
Justifier qu'un ajustement affine de $y$ en $t$ n'est pas pertinent.
-
On pose $z = \ln(y - 28)$.
Recopier et compléter le tableau. Les valeurs de $z$ seront arrondies au centième.Temps $t$ (minutes) 0 1 2 3 4 5 6 Température $y$ (°C) 150 113 82 65 52 44 40 $z=\ln(y-28)$ 4,80 4,44 -
On note $r$ le coefficient de corrélation de la série $(t ; z)$.
On sait que $r \approx -0,999$.
Sur la base de cette information, répondre aux deux questions suivantes en justifiant.-
La corrélation de la série $(t ; z)$ est-elle bonne ?
-
Le nuage de points $(t ; z)$ a-t-il une allure croissante ?
-
-
Déterminer l’équation de la droite de régression linéaire de $z$ en $t$ , selon la méthode des moindres carrés, sous la forme $z = at + b$.
Les coefficients $a$ et $b$ seront arrondis à $10^{-1}$. -
En déduire une expression de $y$ en fonction de $t$ sous la forme $y = C e^{-0,4t} + 28$, où $C$ est une constante que l’on arrondira à l’unité.
-
En utilisant l'ajustement non affine de la question précédente, estimer l'instant à partir duquel la température du matériau devient inférieure à 50 °C.
-
En utilisant le même ajustement non affine, déterminer la température moyenne du matériau durant les 6 premières minutes qui suivent la sortie du four. Arrondir au dixième.
La fabrication de verre minéral résulte d’une fusion de trois éléments (quartz, potasse et oxyde). Tous ces éléments sont chauffés jusqu’à leur température de fusion de 1 500 degrés Celsius dans un four à cuve de vitrification, puis brassés pendant plusieurs heures. Le verre liquide est ensuite acheminé à une presse automatique qui produit des ébauches de verres, lesquels sont refroidis lentement jusqu’à température ambiante dans un four de recuit.
On a mesuré la température du verre minéral dans la cuve de vitrification depuis le début du processus de chauffage jusqu’à la fusion. On obtient les résultats suivants :
| Temps (en minutes) | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|---|---|---|---|
| Température du verre (en degrés Celsius) | 24 | 354 | 614 | 816 | 943 | 1066 | 1395 | 1459 | 1491 |
Représentation de la série $(t ; T )$ :
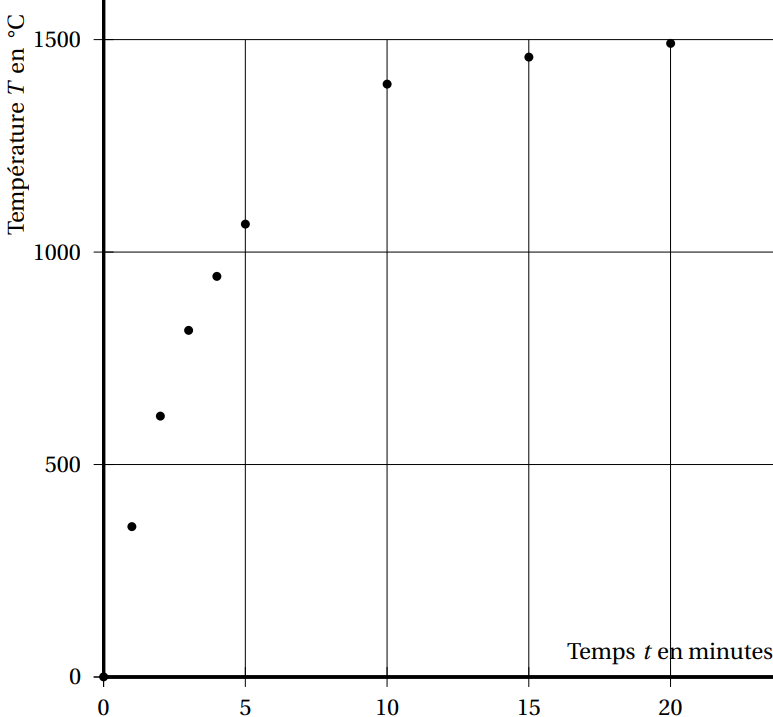
Le coefficient de corrélation linéaire de la série $(t ; T )$ est $r_1 \approx 0,865$.
L’allure du nuage de points représentant la série conduit à procéder à un changement de variable, en
posant : $z=\ln\left(\dfrac{1500}{1500-T}\right)$.
On obtient le tableau de valeurs suivant (les résultats ont été arrondis à $10^{-3}$ près) :
| Temps (en minutes) | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|---|---|---|---|
| Température du verre (en °C) | 24 | 354 | 614 | 816 | 943 | 1066 | 1395 | 1459 | 1491 |
| z | 0.016 | 0.269 | 0.527 | 0.785 | 0.991 | 1.240 | 2.659 | 3.600 | 5.116 |
-
Calculer le coefficient de corrélation linéaire $r_2$ de cette nouvelle série $(t ; z)$.
-
Expliquer pourquoi le changement de variable est pertinent.
-
Déterminer une équation de la droite de régression de $z$ en $t$ selon la méthode des moindres carrés, sous la forme $z = at +b$, où $a$ et $b$ sont arrondis au millième.
-
En déduire, en utilisant le changement de variable, une expression de $T$ en fonction de $t$ de la forme $T = A e^{-0,251t} +1500$, où $A$ est arrondi à l’unité.
-
Utiliser l'ajustement obtenue à la question précédente pour intrapoler la température du verre au bout de 12 minutes.
-
Utiliser ce même ajustement pour savoir à quel moment le verre atteint la température de 1496°C.
Est-ce une interpolation ou une extrapolation ?
On cherche à évaluer l’effet d’un pesticide que l’on peut trouver dans les rivières, sur la diminution de la fertilité d’une population de poissons. Pour cela un laboratoire va disposer huit aquariums, contenant chacun dix poissons de la même espèce et de l’eau avec différentes quantités de ce pesticide. Au bout d’un mois on relève le nombre total d’œufs pondus par les poissons des différents aquariums et on obtient les résultats suivants :
| Numéro de l’aquarium | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Concentration en pesticide (en mg/L) ($x_i$) | 0 | 1 | 4 | 5 | 6 | 7 | 8 | 10 |
| Nombre d’œufs pondus dans le mois ($N_i$) | 249 | 248 | 246 | 230 | 130 | 50 | 40 | 35 |
Un ajustement affine ne semblant pas approprié, on effectue le changement de variable : $y = -\ln\left(\dfrac{250}{N}-1\right)$.
-
Recopier et compléter le tableau ci-dessous en arrondissant les résultats à $10^{-3}$ :
Numéro de l’aquarium 1 2 3 4 5 6 7 8 Concentration en pesticide (en mg/L) ($x_i$) 0 1 4 5 6 7 8 10 Nombre d’œufs pondus dans le mois ($N_i$) 249 248 246 230 130 50 40 35 $y_i=$ $-\ln\left(\dfrac{250}{N_i}-1\right)$ 5,52 0,08 -
Déterminer le coefficient de corrélation linéaire de la série statistique $(x_i ; y_i)$. Arrondir à $10^{-3}$.
Interpréter le résultat. -
Déterminer une équation de la droite d’ajustement de la série statistique $(x_i ; y_i)$ par la méthode des moindres carrés sous la forme $y = ax + b$. On arrondira $a$ et $b$ à $10^{-3}$.
-
On note $N(x)$ la fonction modélisant le nombre d’œufs pondus dans un aquarium en un mois, en fonction de la concentration $x$ en pesticide (en mg/L).
-
En s’aidant du changement de variables $y=-\ln\left(\dfrac{250}{N}-1\right)$, vérifier que $N(x)$ est solution de l’équation $\dfrac{250}{N(x)}-1=e^{0,857x-5,905}$.
-
En déduire que l’expression de la fonction $N$ est : $N(x)=\dfrac{250}{1+e^{0,857x-5,905}}$.
-
-
La concentration efficace médiane notée CE50 est la concentration qui correspond à une diminution de 50 % du nombre d’œufs pondus par mois par rapport à une eau sans pesticide.
Déterminer cette concentration CE50 à $10^{-1}$ près. Expliquer votre démarche. -
Estimer, à l’unité près, le nombre moyen d’œufs pondus par mois, pour des concentrations en pesticide comprises entre 4 et 6 mg/L.
Pour les deux questions suivantes, on admet que la fonction $N$ modélise le nombre d’œufs pondus par mois dans un aquarium, en fonction de la concentration $x$ en pesticide (en mg/L) sur l’intervalle $[0; 50]$.
Demander le programme
-
Savoir la signification d'un point moyen d'une série statistique à deux variables.
-
Savoir ce qu'est la méthode des moindres carrés.
-
Savoir le rôle du coefficient de corrélation linéaire pour comparer la qualité de deux ajustements.
-
Savoir la définition d'une interpolation.
-
Savoir la définition d'une extrapolation.
-
Savoir représenter sur Geogebra un nuage de points associé à une série statistique à deux variables.
-
Savoir obtenir sur Geogebra le point moyen d'une série statistique à deux variables.
-
Savoir obtenir sur Geogebra un ajustement affine d'une série statistique à deux variables.
-
Savoir réaliser un changement de variable pour réaliser un ajustement se ramenant à un ajustement linéaire.
-
Savoir utiliser un ajustement pour réaliser une interpolation ou une extrapolation.
-
Savoir obtenir sur Geogebra le coefficient de corrélation linéaire d'une série statistique à deux variables.
-
Savoir faire la différence entre une corrélation forte et un lien de causalité.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International